The Sand and the Swimming Pool

Here’s an interesting problem that is directly applicable to the behaviour of light. Suppose that you want to get from point A to point B, what is the fastest route? The most common answer is “in a straight line” but this isn’t always true. Let’s put our points A and B on a sandy beach that has a swimming pool running through the middle of it, as shown in the diagram below.

Given that you can run on the sand much faster than you can swim through the water, what route should you take in order to get from A to B in the least possible time? The dotted black line shows the straight-line route and the next most common answer, which involves crossing the swimming pool in the most direct way, is shown as a red dotted line.

Clearly the red route is longer in distance but is it a quicker path? Let’s put in some numbers and do a couple of calculations to find out…

Let’s say that the vertical separation of these two points is 20 m and their horizontal separation is 40 m. Let’s also say that the width of swimming pool is half the vertical separation (10 m). Finally, we’ll say that we can run five times as fast as we can swim: let’s say that’s 5 m/s for running, meaning that we can swim at 1 m/s. Note that these are just example numbers that will allow us to do the calculation.

To calculate the time for the red route, we add the times for each part of the route, using the familiar equation which states that time is equal to distance divided by speed.

The stages to sum are a downward run across 5 m of sand followed by a downward swim through 10 m of water then another downward run across 5 m of sand followed by a ninety-degree turn before a final 40 m run across the sand.

Total time for red route = (5/5) + (10/1) + (5/5) + (40/5) = 20 seconds

The black route is a bit harder to calculate as it involves running in a diagonal direction so we’ll have to calculate the diagonal distances before we can calculate the individual (and total) times. The simplest way to do this is by using the idea of similar triangles and divide the full length of the diagonal into proportional sections.

The total length of the diagonal (black line) is given by the square-root of (20² + 40²) which gives 44.72 m. This is divided into quarters, to give sections that are 11.18 m long. The first and last quarters correspond with the first and last parts of the journey, over sand, and the middle two quarters are the distance through the water. We can simply substitute the distances for these three sections into our equation for time to get the total value, as follows;

Total time for black route = (11.18/5) + (22.36/1) + (11.18/5) = 26.83 seconds

Clearly the straight-line (black) route is not the fastest in this case!

But it seems unlikely that the red route is the fastest of all possible routes simply because it is actually the longest route that we could take (assuming we confine ourselves to straight lines).

The question of fastest routes relates directly to refraction of light, where we know that light bends towards the normal (takes a more direct route) when it crosses the boundary into a medium where it travels slower than before. It turns out that there is a rule, known as Snell’s Law, that allows the change in angle of travel to be predicted using the following equation;

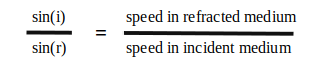
Snell’s Law isn’t in our syllabus but it’s worth knowing that it defines the distance travelled by a wave on two different sides of a boundary in the same amount of time. In other words, if a wave crosses a boundary from a medium where it travels quicker to one where it travels slower, the angle of the wave will change so that the distance travelled in each moment of time is reduced in the same proportion as the decrease in speed. This keeps the wave “together” as a continuous transfer of energy even when the wave speed decreases.

To make life easier, we refer to the relative refractive index (symbol, n) of a medium as the ratio of the speed of light in air divided by the speed in the other medium. Glass, for example, has a typical value of n=1.3 so we know that light travels 1.3 times faster in air than in glass (or in glass it travels at 1/1.3, or about 77%, of its speed in the air).

You can explore refraction, and the effect of changing the refractive index, using the excellent PhET simulation at https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_en.html.